A Kernel Dev's Approach to Improving Mutt's Performance - Part 2
In the last post I talked about tuning mutt to reduce the time to open my LKML folder, and showed that a 9x speedup was possible simply by changing some configuration parameters. In this post, we’ll investigate the reason that mutt freezes whenever new mail arrives in the LKML folder.
I noticed that when mutt locks up top(1) reports it consuming 100%
CPU, which suggests that we can use the cpu-cycles perf event to
gather a profile for mutt and figure out where those cycles are going.
I triggered a remote mail fetch while simultaneously running perf in another window:
$ perf record -e cycles -p `pidof mutt`Which produced the following profile:
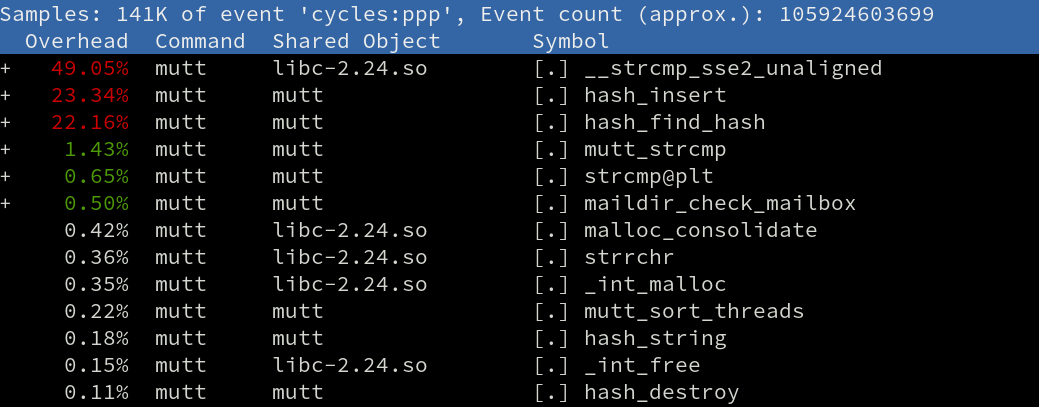
That’s basically 100% of the time being spent working with a hash table. When checking for new mail, mutt creates a hash table and adds the filenames of all files in the LKML directory, and that’s where all the cycles are going when mutt freezes.
The top three items in the above perf profile are related to two separate hashing actions:
- Hash element insertion and collision handling
- Hash element lookup
To really get to grips with the hashing used by mutt I pulled all the relevant code out into a separate program, and added some code to print various statistics to guide me in figuring out how I might eliminate the freeze (or at least reduce it).
$ time -p hashinsert
real 19.77
user 19.57
sys 0.18It takes 20 seconds just to build the hash table, never mind searching for elements. To understand why it takes so long let’s deconstruct the code for inserting hash elements.
Hash insertion and collision handling
The following is snippet of C code is the hash_insert() code from
mutt.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
static void
hash_insert(struct hash_elem **table, const char *key, void *data)
{
struct hash_elem *elem = malloc(sizeof(*elem));
struct hash_elem *tmp, *last;
unsigned int hash;
unsigned long collisions = 0;
if (!elem)
abort();
elem->key = key;
elem->data = data;
hash = hash_string(key, HASH_TABLE_SIZE);
for (tmp = table[hash], last = NULL; tmp; last = tmp, tmp = tmp->next, collisions++) {
int r;
r = strcmp(tmp->key, key);
if (r == 0) {
free(elem);
abort();
}
if (r > 0)
break;
}
As you can from line 19, strcmp() is invoked whenever there’s a hash
collision that requires walking the collision chain, and we saw in the
perf cpu-cycles event profile that roughly 50% of the freeze time is
spent dealing with hash collisions. Large numbers of collisions could
be caused by a couple of things:
- Hash table isn’t sized correctly
- Hashing function doesn’t uniformly distribute hash keys
So before we go any further, let’s take a look at the code that creates the hash table:
/* we create a hash table keyed off the canonical (sans flags) filename
* of each message we scanned. This is used in the loop over the
* existing messages below to do some correlation.
*/
fnames = hash_create (1031, 0);Umm.. this hash table has 1031 slots? My LKML directory has 65,1140 files in it! No wonder I’m seeing lots of collisions. Even if the hashing function used in mutt was perfect, there are still far too few slots for the number of entries we’re inserting. But how many slots should the table have?
Hash table size
In Section 6.4 of Vol III of The Art of Computer Programming, Donald Knuth talks about the load factor which states that if you wish to insert \({M}\) entries, and your hash table has \({N}\) slots, then the average collision chain length is:
\[\begin{align*} load\_factor = \frac{M}{N} \end{align*}\]Plugging in the values for mutt’s hash table size and the number of entries in my LKML directory shows immediately why so much time is spent walking the collision chain:
\[\begin{align*} load\_factor = \frac{M}{N} = \frac{651140}{1031} = 631.56 \end{align*}\]That is, on average, a slot in the hash table will have a collision change length of 632!
Hashing function distribution
Because we’re dealing with averages, the above equation does assume that mutt’s hashing function produces uniformly distributed keys, such that each slot is equally likely to be used for inserting an element.
Knuth warns us thus:
“Finally, we need a great deal of faith in probability theory when we use hashing methods, since they are efficient only on average, while their worst case is terrible! - Donald E. Knuth
I added code to the hashinsert program to dump the collision chain length for every slot in the hash table, which I then used to produce the following histogram:
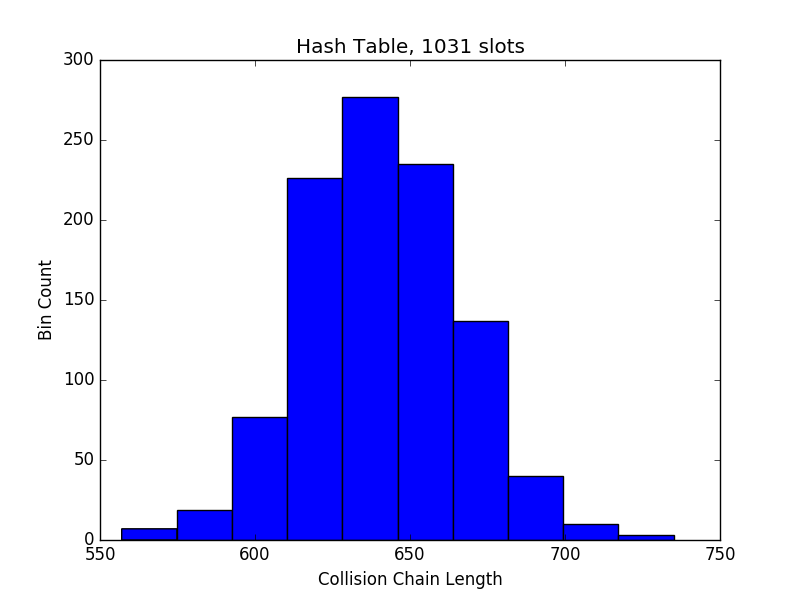
The mean collision chain length is 640.88, which is fairly close to the value predicted by the equation above.
To see how changing the hash table size might improve element insertion time, I measured a number of sizes:
| Hash Slots | Total Insertion Time (secs) | Slots Formula |
|---|---|---|
| 1302280 | 0.38 | \({2N}\) |
| 651140 | 0.38 | \({N}\) |
| 40696 | 0.84 | \(\frac{N}{16}\) |
| 20348 | 1.34 | \(\frac{N}{32}\) |
| 10174 | 2.41 | \(\frac{N}{64}\) |
| 5087 | 4.24 | \(\frac{N}{128}\) |
| 2543 | 8.11 | \(\frac{N}{256}\) |
| 1271 | 18.40 | \(\frac{N}{512}\) |
| 1031 | 19.77 | \(\frac{N}{631}\) |
Note: Prime numbers are sometimes used as the hash table size because doing so helps to more evenly distribute elements among the slots, and can make up for a poor hash function choice. I re-ran the test with (next highest) prime slot numbers and the results were pretty much the same.
Interestingly the first item in the above table, using \({2N}\) slots, didn’t actually result in a reduction in insertion time, even though it should reduce the chances of collisions.
But that’s fine, it makes the selection of number of slots that much easier.
Hash lookup
The other side of the coin when working with hash tables is pulling
elements out by performing a lookup using a key. For the hash table
code used in mutt (and my toy program) the speed of the lookup operation is
all about strcmp().
Unlike the insertion operation where we could increase the table size
and avoid having to handle a slot collision (and executing
strcmp()), we must necessarily compare two keys when performing a
lookup.
You can see from the perf profile at the very top of this article that
the implementation of strcmp() uses __strcmp_sse2_unaligned(). A
good initial question would be “Can we improve performance by aligning
the keys strings?” A quick google shows that eliminating the
misaligned accesses won’t make a noticable difference on modern Intel
CPUs, i.e SandyBridge and
newer, and I’m
running mutt on an Intel Core i7-5600U which is part of the Broadwell
family.
But then, if I’m running such a modern CPU, perhaps I can use a newer version of SSE, since SSE2 was introduced in 2001.
It turns out that glibc doesn’t use SSE4.2 for the strcmp*() family
of functions on openSUSE Tumbleweed (only strcasecmp()). Another
option to make use of SSE4.2 would be to switch to using memcmp()
assuming we know exactly how many bytes of the key we want to compare
a priori (credit goes to Michael Matz at SUSE for this suggestion).
Unfortunately mutt doesn’t calculate that length because its hash function works a byte at a time:
static unsigned int
hash_string (const unsigned char *s, unsigned int n)
{
unsigned int h = 0;
while (*s)
h += (h << 7) + *s++;
h = (h * SOMEPRIME) % n;
return h;
}Where n is the table number of slots in the hash table. So trivially
switching to a newer SIMD technology seems to be out.
Now, some readers may have noticed that I never re-profiled the test
application after increasing the hash table size. The reason is that I
was only looking at the low-hanging fruit for improving lookup time –
things that could be done easily without much effort (I was also
curious to learn whether switching strcmp() implementations was
possible).
Given that I’ve run out of simple tricks, let’s go back and check on the new lookup cost since it’s impossible to tell whether it’s still an issue or not with the adjusted number of slots.
Calculating the total insertion and lookup time shows that we can pretty much call it quits for our optimisation efforts:
| Hash Slots | Total Insertion Time (secs) | Total Lookup Time (secs) |
|---|---|---|
| 1302280 | 0.337 | 0.332 |
| 651140 | 0.364 | 0.373 |
| 40696 | 0.818 | 0.823 |
| 20348 | 1.303 | 1.303 |
| 10174 | 2.230 | 2.237 |
| 5087 | 4.91 | 4.209 |
| 2543 | 8.116 | 7.813 |
| 1271 | 15.180 | 15.208 |
| 1031 | 18.393 | 19.211 |
The times are quite symmetrical when comparing insertion and lookup.
Folding it back into mutt
Below is the change I made to mutt’s maildir_check_mailbox() to take
into account the number of files my the LKML directory when building
the hash table. With it, I no longer see any lockup when new mail
arrives:
Simple, no?